凸形能否有兩個等弦點

—— 李露萍

摘 要：“凸形能否有兩個等弦點”是幾何學(xué)歷史長河中遺留下來的未解決的數(shù)學(xué)問題之一，為了探究這個問題，本文從不存在等弦點的正方形出發(fā)，再推廣到正多邊形上；再借助于單連通的連續(xù)且直到二階可導(dǎo)的上凸函數(shù)為工具，假設(shè)在至少存在一個等弦點且弦長恒為的基礎(chǔ)上，通過對上凸函數(shù)關(guān)于等弦點的對應(yīng)函數(shù)的一階導(dǎo)數(shù)的判斷，得出當(dāng)時，若，則對角函數(shù)隨著的不同而不同，故不存在等弦點；若時，并通過對二階導(dǎo)數(shù)的討論，得到相應(yīng)的結(jié)論。

關(guān)鍵詞：凸函數(shù)；對角函數(shù)；等弦點；一階導(dǎo)數(shù)；二階導(dǎo)數(shù)

Abstract："Convex can have two chord point＂is a geometric history left unsolved mathematical problems. To explore this issue, the paper never existed chord point square starting, and then extended to the regular polygon; and with the help of the simply connected continuous and convex function picture until the two order derivative as a tool. Assuming there is at least one chord point and chord length is constantbasis,by first order derivative corresponding function of convex function on the chord point of judgment, when the ,if , is diagonal function with is different, so there is no chord point. If the , and through the discussion of the two order derivative, corresponding conclusions are obtained.

Key words：Convex function；Diagonal function；Chord point；Derivative；Two order derivative

1 引言

組合幾何正式成為一門數(shù)學(xué)分支只有半個世紀的歷史，但是與組合幾何有關(guān)的問題卻可追溯到遙遠的歷史深處。絕大多數(shù)需要解決的幾何問題都產(chǎn)生于實際要求，而“凸形能否有兩個等弦點”是幾何學(xué)歷史長河中遺留下來的未解決的數(shù)學(xué)問題之一。對凸形問題的探究又離不開用凸函數(shù)來表達，而凸函數(shù)是一類具有顯著幾何特征的函數(shù)，在線性規(guī)劃、最優(yōu)控制、不等式等領(lǐng)域都有著非常重要的應(yīng)用。1905年丹麥數(shù)學(xué)家Jensen^[1]首次給出了凸（凹）函數(shù)的定義，開創(chuàng)了凸（凹）函數(shù)研究的先河。在現(xiàn)有的文獻中，對凸函數(shù)的研究各方面的討論都近乎完善，也得到了很多有用的結(jié)論，但是在對于凸形的邊界凸函數(shù)及等弦點的研究卻鮮有所聞。所以需要尋找探究凸形邊界函數(shù)及等弦點的相關(guān)問題。

本文將借助于單連通的連續(xù)且直到二次可導(dǎo)等條件下的凸函數(shù)^[2]~[7]來考慮特殊的凸形能否有兩個等弦點，從一階導(dǎo)數(shù)和二階導(dǎo)數(shù)的角度，分析探究凸形能否有等弦點甚至是能否有兩個等弦點。

2 預(yù)備知識

為了進一步探究“凸形能否有兩個等弦點”這個問題，我們需要回顧一下單連通、一階導(dǎo)數(shù)及二階導(dǎo)數(shù)的求法等的相關(guān)知識。

2.1 凸形

定義2.1^[8] 設(shè)集合，若對于 ，，有

，

則稱為凸集。

定義2.2^[8] 如果對于點集中任意兩點、，線段上的點都屬于點集，那么成為凸集。

定義2.3^[8] 有界閉集，如果是凸集，就成為凸形。

2.2 等弦點

定義2.4^[8] 一個封閉凸平面曲線之內(nèi)的點，且經(jīng)過那個點的所有弦具有相同的長度。例如，圓的圓心是這個圓的等弦點。

2.3 單連通

定義2.5^[9] 我們用 記復(fù)平面以及用 記復(fù)擴充平面。一個連通開集 被稱為單連通區(qū)域。

2.4 參數(shù)方程表示函數(shù)的求導(dǎo)法

2.4.1 參數(shù)方程表示函數(shù)的一階導(dǎo)數(shù)^[10]

在解析幾何中，我們遇到過曲線的參數(shù)表示法，若為參數(shù)，那么

就代表平面上的一條曲線。設(shè)的反函數(shù)為，并且沒它滿足反函數(shù)的條件，于是把看做復(fù)合函數(shù)

。

并利用復(fù)合函數(shù)和反函數(shù)的求導(dǎo)法則，就有

，

這就是參數(shù)方程所表示函數(shù)的求導(dǎo)方法。

當(dāng)參數(shù)給出時，就可得到在對應(yīng)點的倒數(shù)的值。

例2.1 橢圓的參數(shù)方程是，求。

解 于是有

．

由此可知，當(dāng)時，，即在點橢圓有水平切線。

2.4.2 參數(shù)方程表示函數(shù)的二階導(dǎo)數(shù)^[10]

參數(shù)方程求二階導(dǎo)數(shù)的方法：

由前已知

，

那么

。

例2.2 設(shè)求二階導(dǎo)數(shù)

解 由例2.1可知：

，

。

3 證明

3.1 正多邊形

由凸形的概念可知，正多邊形是一種特殊的凸形，下面對正多邊形進行討論，以正方形為例。

3.1.1 正方形

如圖3-1中，我們以邊長為1的正方形為例，以正方形的底邊建立直角坐標(biāo)系，假設(shè)存在等弦點，且弦長恒為，則在一條直線邊上取一點的與等弦點的連線，取線段長為，在該直線邊上再取異于的點，，····，由于過等弦點的弦長長度相等，則易知通過該直線邊上的點得到的是一條曲線，這與正方形的性質(zhì)相矛盾，故命題假設(shè)存在等弦點不成立。

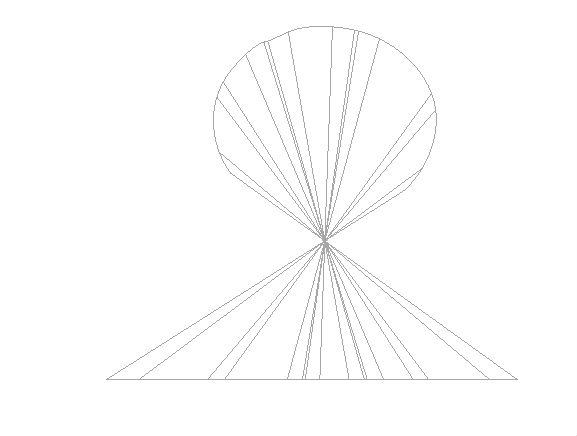
圖3-1

3.1.1 正多邊形

正多邊形的每條邊都是直線邊，而由正方形不存在等弦點的證明可知，若正多邊形存在等弦點，那么正多邊形的直線邊關(guān)于等弦點的對應(yīng)邊則是曲線邊，這與正多邊形的性質(zhì)不符，所以正多邊形也不存在等弦點。

3.2 單連通的連續(xù)且直到二階可導(dǎo)的凸形

3.2.1 原理

假設(shè)該凸形至少存在一個等弦點，設(shè)為，再過點作坐標(biāo)軸作為軸建立直角坐標(biāo)系，該凸形的邊界函數(shù)在軸附近存在連續(xù)且直到二階可導(dǎo)的上凸函數(shù)，在此上凸函數(shù)上任取一點，通過作弦長恒為的對角函數(shù)，若對于不同的取值的作出來的對角函數(shù)都相同，則可知這個上凸函數(shù)可能至少存在兩個等弦點；但反之，該種凸形就一定不存在兩個等弦點。

3.2.2 假設(shè)：

（1）單連通凸形的邊界函數(shù)是連續(xù)的，并且是直到二階可導(dǎo)的上凸函數(shù)；

（2）該上凸函至少存在一個等弦點，設(shè)為；

（3）弦長恒為；

（4）其中，為常數(shù)，，是變量，取參數(shù)；

則對于邊界上凸函數(shù)關(guān)于等弦點的對角函數(shù)為：

由，是關(guān)于的參數(shù)函數(shù)，故令

，

其中由（2）可得：

···········（３）

將（3）式帶入（1）式可得：

，

所以

，

所以該對角函數(shù)的一階導(dǎo)數(shù)為：

，

其中：

；

；

所以當(dāng)時，有 ：

；

；

；

若當(dāng)時，則對角函數(shù)隨著的取值的變化而不相同，故在

此種情況下，上凸函數(shù)不存在兩個等弦點；換句話說，即為等弦點到凸形邊界的連線段與凸形邊界的交點處的切線都不相垂直的凸形不存在兩個等弦點。

若當(dāng)時，則有：

；

又上凸函數(shù)的對角函數(shù)的二階導(dǎo)數(shù)為：

，

其中：

；

；

；

；

則當(dāng)時，令

，

那么可得

；

；

；

；

則

；

即有

；

因為對應(yīng)函數(shù)是由上凸函數(shù)所求的對角函數(shù)，故函數(shù)必定為下凸函數(shù)，即有：

，

即恒有

，

其中:

；

由上式可知，只有中有變量，其中，和均為常量，所以要想證明凸形是否存在兩個等弦點，即轉(zhuǎn)證為證明關(guān)于等弦點的對角函數(shù)在不同取值的時，仍是同一函數(shù)；從而轉(zhuǎn)為證明凸形的二階導(dǎo)數(shù)關(guān)于的取值不同時，所得到的值任然相等即可，進而到對對角函數(shù)的二階導(dǎo)數(shù)的單調(diào)性的判斷。

故上凸函數(shù)的對角函數(shù)的二階導(dǎo)數(shù)對有求導(dǎo)為：

；

又因為函數(shù)是上凸函數(shù)，所以其二階導(dǎo)數(shù)恒有，則恒有

；

且又由題可知：

（即），，；

所以有

；

那么

；

因為是上凸函數(shù)的二階導(dǎo)數(shù)，且，所以，，從而有，，則分子即為一個小于0的數(shù)加上一個大于0的數(shù)，不能直接判斷其分子的正負，就更不能判斷二階導(dǎo)數(shù)對的導(dǎo)數(shù)的判斷；即在此種情況下不能判斷凸形對應(yīng)函數(shù)的二階導(dǎo)數(shù)對的不同取值時值的變化情況，所以在此種條件下不能判斷該種凸形能否有兩個等弦點。

4 結(jié)論

由對正方形的是否含有等弦點的推導(dǎo)可知，正多邊形不存在等弦點；若考慮在至少存在一個等弦點的凸形中，對于邊界函數(shù)是單連通的連續(xù)的且直到二階可導(dǎo)的凸函數(shù)的凸形，若關(guān)于等弦點的對角函數(shù)在時的一階導(dǎo)數(shù)不等于0，那么這個凸函數(shù)關(guān)于等弦點的對角函數(shù)會隨著取值的變化而變化，故在此種情況下，該種凸形沒有兩個等弦點，也就是說，當(dāng)已知等弦點到邊界函數(shù)的連線段與該交點處的切線不相垂直時，凸形不存在兩個等弦點；若關(guān)于等弦點的對角函數(shù)的一階導(dǎo)數(shù)等于0，其二階導(dǎo)數(shù)關(guān)于的導(dǎo)數(shù)在為

，

由條件可知分母，而分子中第一部分，第二部分，一個小于0的數(shù)加上一個大于0的數(shù)，不能判斷其大小，故無法判斷其二階導(dǎo)數(shù)在取值不同時的變化情況，所以在此種條件下不能判斷該種凸形能否有兩個等弦點。

參考文獻：

[1] 張慧玲. 連續(xù)凹函數(shù)的幾個性質(zhì)[J]. 廊坊師范學(xué)院學(xué)報（自然科學(xué)版）, 2009, 1674-3229(01).

[2] 蒲義書, 陳露. 凸函數(shù)概述[J]. 高等數(shù)學(xué)研究, 2006(04).

[3] 張占通，譚杰新. 連續(xù)函數(shù)為凸函數(shù)的兩個充要條件[J]. 維普, 1994.

[4] 王霞, 江曉武. 連續(xù)凸函數(shù)的判據(jù)及幾何特征[J]. 數(shù)學(xué)實踐與認識, 2006(12).

[5] 曾明,范周田. 關(guān)于凸函數(shù)定義的幾點思考[J]. 高等數(shù)學(xué)研究. 2010(04)．

[6] 劉仁義. 關(guān)于凸函數(shù)的判定[C]. 九江師專學(xué)報, 1999.

[7] 李世杰. 連續(xù)函數(shù)的凸性[J]. 上海中學(xué)數(shù)學(xué), 2005(03).

[8] 單墫. 組合幾何[M]. 上海教育出版社, 1995.5.

[9] 謝樺. 單連通空間的一些性質(zhì)[J]. 龍巖師專學(xué)報, 1993(03).

[10] 歐陽光中，朱學(xué)炎，金福臨，陳傳章. 數(shù)學(xué)分析[M]. 第三版. 高等教育出版社.2007.